Physics Department [Return to Examples]
KINEMATICS EXAMPLE 9
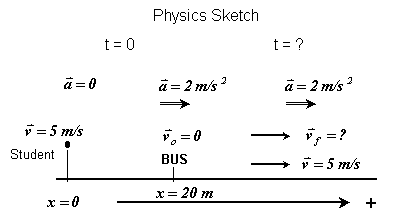
A student, who is running to catch his bus, sees the bus start to pull away from the stop. He is 20 m away from the stop and running at his top speed of 5 m/s. If the bus accelerates at 2 m/s2, can he catch the bus?
Given: (By the way, we identify the given
information explicitly, so: we can be
sure we know what quantities are involved, we are sure of using appropriate
symbols to represent the quantities, and we have all quantities with consistent
units.) Initial separation between
student and bus -- 
student’s speed (we
assume he runs at a constant speed) -- 
student’s acceleration -- 
(we know his speed is
constant, and we assume he runs in a straight line), initial speed of the bus
-- 
(since it was
stopped), acceleration of the bus -- 
Unknown: (Explicitly identifying the unknown(s) including the proper symbol and units, is necessary so we can be clear about our goal. Being aware of our goal allows us to check our progress, and will alert us when we go astray, so we can redirect our efforts.) This problem is one where identifying the unknown is not obvious; in fact, this step is critical for the solution of this problem. As the problem is stated, what we seem to need is a yes or no, i.e., yes, he catches the bus; or no, he does not. But how do we determine this? We assume he will catch the bus and determine when that happens. That is, the time when he catches the bus becomes our unknown – t = ? s. (If the time we get is impossible, for example, if the time turns out to be negative, that would mean he couldn’t catch the bus. We will look at this issue in more detail later).
Physical (Mathematical) Principles and/or Ideas: constant velocity motion, and constant acceleration motion.
Solution: Now we know the situation – we have one
“object”, the student, undergoing constant velocity motion and the other
undergoing constant acceleration motion – we know what to find -- the time when
he catches the bus. But how do we do
that? First, we translate the phrase,
“he catches the bus” to what this means in terms of physics. That has been done in the right diagram in
the physics sketch. The translation is
that if the student is able to catch the bus, then he and the bus will have the
same x position, i.e., they will be at the same location. At this point, we can get some
equations. The equation for the position
of an object undergoing constant velocity motion is 
And the equation for
the position of an object undergoing constant acceleration motion is 
We know 
for the bus and 
but what value do we
put into the equation for 
The answer comes
from the physics sketch. Notice that we
placed the student at the point 
that is 
Since the separation
distance between the student and the bus is 20 m, we now know 
So we have:
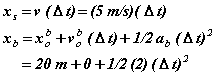
Next, we set these two equations equal to each other and
solve for 
Since we can see that the units for all three terms are m,
as they must be, we will leave the units off from here on. (Why must all of these terms have units of
m?) Rewriting the equation and taking 
so 
can be replaced by 
, we have:
This is a quadratic equation, so we apply the quadratic formula:
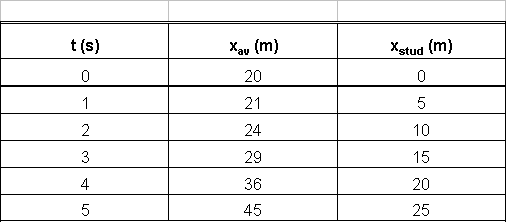
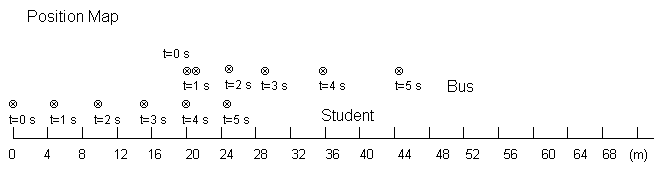
Since we have a negative number under the radical, the times are imaginary, i.e., the student cannot catch the bus. Let us check this out with a pair of position maps and position versus time graphs. First, we set up a chart for the positions of the two objects for the first five seconds.
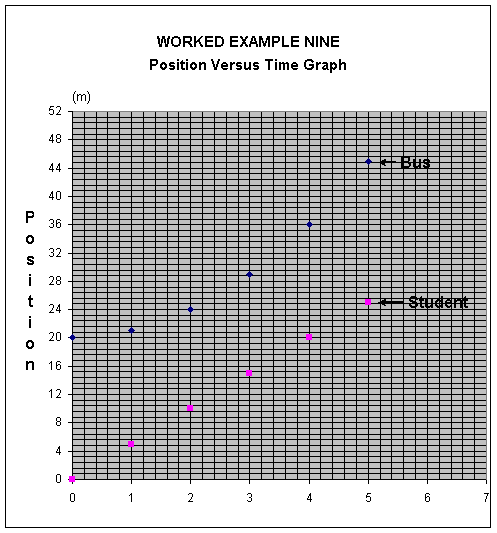
It is always worthwhile, when you have solved a problem, to ask yourself, “What if
. . . . . . . . . . . . . . . were changed in the following way . . . . . . . . . . . . . . ? putting several different things in each blank. One obvious example from this problem is:
How fast would the student have to run to be able to catch the bus in this situation? OR
How slow would the bus’ acceleration have to be for the student to catch the bus?