KINEMATICS EXAMPLE 4

 

 

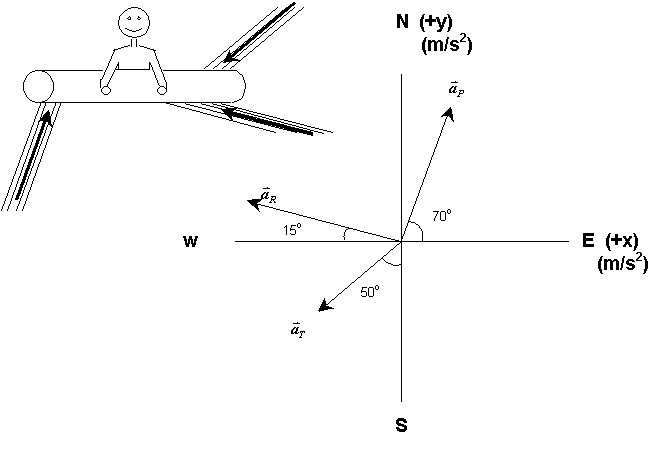
A flood victim clinging to a log comes to a place where three streams meet.  Each stream tries to accelerate the log in a different direction and at a different rate.

Stream P would accelerate it at 14 m/s²  70^o north of east.  Stream R would accelerate it at 18 m/s²  15^o north of west.  And Stream T would accelerate it at 11 m/s²  50^o west of south. 

What will the actual acceleration of the log be?

 

Given:            

                       

                       

 

Unknown:       The net, or resultant, acceleration,

 

Physical Situation                                                                 Physics Sketch

 

 

 

 

Physical (Mathematical) Principles and Ideas:  rules for adding vectors, trigonometric functions and Pythagorean theorem.

Solution:         This problem doesn’t involve anything fundamentally different from problem three.  That means we want to carry out the same “program” here as we did in problem three.

 

a)         Our first task is to find the x and y components of three vectors.  (What difference does it make that the vectors here are accelerations?  Why?)

For  we get:

 = (cos 70^o)(hypotenuse) = (14 m/s²)(cos 70^o) = +4.8 m/s²

 = (sin 70^o)(hypotenuse) = (14 m/s²)(sin 70^o) = +13.2 m/s²)

or we could write these as  = 4.8 m/s² (+x) and  = 13.2 m/s² (+y).

For  we find:

 = (hypotenuse)(cos 15^o) = (18 m/s²)(cos 15^o) = -17.4 m/s²

 = (hypotenuse)(sin 15^o) = (18 m/s²)(sin15^o) = +4.7 m/s²

We have to be a little careful getting the components for  since the angle given is with the y axis, not the x axis.  For this angle, the x component is the opposite side and the y component is the adjacent side.  So we get:

                         = -(sin 50^o)(hypotenuse) = -(11 m/s²)(sin 50^o) = -8.4 m/s²

                         = -(cos 50^o)(hypotenuse) = (-11 m/s²)(cos 50^o) = -7.1 m/s²

 

b)         This step of the “program” requires us to add the x components and then add the y components separately.  So we have:

 = 4.8 m/s² + (-17.4 m/s²) + (-8.4 m/s²) = -21.0 m/s²

 = 13.2 m/s² + (4.7 m/s²) + (-7.1 m/s²) = 10.8 m/s²

 

c)         Here we get the vector sum of the x and y components using the Pythagorean theorem.  The magnitude of the resultant acceleration is:

 

                       

 

To find the angle, we can again use the sine, cosine, or tangent.  Let’s use the cosine this time.

 

           

 

Now this is the angle the resultant vector makes with the x axis.  We know it is with the x axis because we used the x component as the adjacent side.  But what quadrant is it in?  Since the x component is negative and the y component is positive, the resultant acceleration is in the second quadrant.  So the answer to our problem is:   = 23.61 m/s² 27.2^o N of W