KINEMATICS EXAMPLE 8

 

A student leans out of a fourth floor window of the science building and sees a certain physics instructor who is coming along the sidewalk below.  She would like to hit this instructor with a water balloon when he is under the window, but she must throw the balloon right now and the instructor will not be below the window until 3 seconds later.  The window is 18 m above the ground.  How can she hit the instructor?

 

Given:             Height from which the water balloon is thrown, height = 18 m, and the time until the target gets in place = 3 seconds, and the acceleration due to gravity on the earth, g = 9.8 m/s².

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

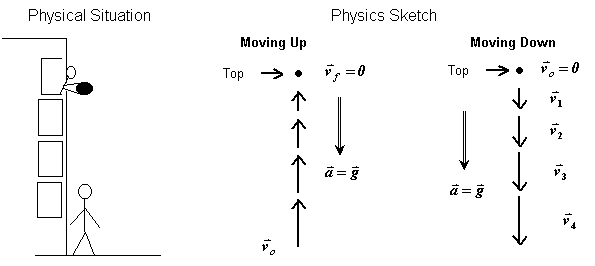
Solution:         If the balloon will take 3 seconds to fall from the window, the student can simply drop the ball.  Since the balloon will undergo constant accelerated motion with the acceleration being 9.8 m/s² and the initial velocity being zero, we can easily compute how long it will take the balloon to fall.

We have: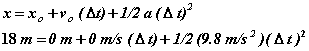                   

                                               

 

So, the student cannot simply drop the balloon.  Neither can she throw the balloon downward because adding an initial downward velocity would reduce the time the balloon is in the air.  But this does suggest the idea of throwing the balloon up since that will add to the time it is in the air.  But how do we determine how fast she needs to throw it upward?

 

We could determine what initial speed she should use by trial and error.  The motion of the balloon can be treated as having two parts, the trip up to the top of the path during which the balloon is slowing down at a constant rate, since the velocity and acceleration have opposite directions, and the trip down from the top during which the balloon is speeding up at the same constant rate it slowed down at on the trip up, since the velocity and acceleration are now in the same direction.  We know the velocity of the balloon at the top is zero because the point where the balloon stops instantaneously is by definition the highest point in the path.  So, for the trip up, the final speed, i.e., the speed at the top, is zero, and for the trip down from the top, its initial speed is zero.

 

Suppose she throws the balloon up at 1 m/s, how long before it hits the ground?  We can find out how long it takes the balloon to get to the top by using the fact that the velocity at the top will be zero (AT AN INSTANT).  So,

becomes       

                                                                                    with    

 

Since the average speed for the trip up will be  the distance from where the balloon is thrown to the top will be:

                                               

 

That means that the top is 18 m + 0.051 m = 18.051 m above the ground.  Since its velocity at that point is zero, the time for the balloon to fall to the ground is given by:

                                               

                                   

                                            

The total time in the air is .102 s + 1.919 s = 2.021 s, which is too short.  Consequently, we know she has to throw the balloon up faster then 1 m/s.

 

For our second trial, let us use 10 m/s.  We follow the same procedure we used for 1 m/s.  The time up to the top is given by:

                                   

 

Since the average speed for the trip up will be 5 m/s, the distance from where the balloon is thrown to the top will be:

                                   

 

That means the top is 18 m + 5.1 m = 23.1 m above the ground.  Since its velocity at that point is zero, the time for the balloon to fall to the ground is given by:

                                   

                                   

The total time in the air is 1.02 s + 2.17 s = 3.19 s, which is too long.

 

At this point, we know the velocity needed to keep the balloon in the air for 3 s is between 1 m/s and 10 m/s, and closer to the latter value.  We could continue with this trial and error process, but there is a better way.  The mathematical equations are actually models of the physical system so we can use the model to answer our question.  However, we need to be very careful that we set the model up correctly.  Since velocity and acceleration are vector quantities, we must use positive and negative signs to indicate directions, and we have to be sure we have the proper directions identified.  Consider the figure below:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

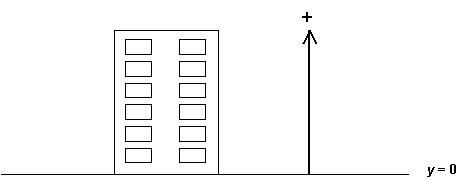
This figure says we are going to take the ground as the point where y = 0, and that vectors whose directions are up will be positive.  The equation we are going to use is:

                                   

The values we are going to put into this equation are:  final position  (the balloon will be on the ground), initial position  (the balloon is initially , when thrown, - 18 m ABOVE the ground), initial velocity  (the balloon thrown upward), the acceleration is --  (as soon as it leaves the student’s hand, the balloon is subject to the acceleration due to gravity which acts on it throughout its motion), and the time interval   So the specific equation for the situation in this problem is:

                                   

 

Notice this is still a vector relationship; the directions are specified by the + and – signs.  Solving for the initial velocity, we get:

                                   

 

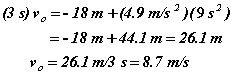
This value is consistent with the information we had from our two trial and error efforts, so it seems very reasonable.