Physics Department [Return to Examples]
KINEMATICS EXAMPLE 3
Two people push on a desk they are trying to move. One person pushes with 35 N at a 50o angle, while the other person pushes with 27 N at a 340o angle. What is the resultant push on the desk?
Given: push
one, 
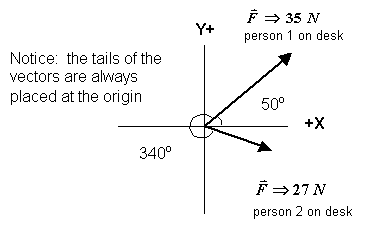Unknown: resultant push, 
Physical (Mathematical) Principles and Ideas: rules for adding vectors, trigonometric
functions and Pythagorean theorem.
Solution: There are several ways to add vectors, which are neither co-linear (i.e., do not lie along a line) nor perpendicular. The one that can be used most easily in the greatest variety of situations is the method of components. A vector, any vector, can always be “broken” down in two (or in three dimensions—three) other vectors at right angles to each other which, when added vectorially using the Pythagorean theorem, “sum” to give the original vector. These two (or three) vectors are called components. Using this idea of components, the general outline for how we solve vector addition problems is the following:
(a) “Break” each vector down into its components along identified axes using trigonometric functions. That is, find the x and y (and when necessary z) components of each vector in the problem. Notice that this process requires orienting the vectors properly on a set of coordinate axes.
(b) Add the components for each of the axes independently, i.e., add the x components to get one “x vector”, add the y components to get one “y vector”, and add the z components to get one “z vector”. Keep in mind that these processes of “adding” components may actually involve subtracting, since components pointing in opposite directions would subtract.
(c) Finally, we add the “x vector”, “y vector” and “z vector”, using the Pythagorean theorem, to find the resultant (sometimes called the net) vector.
We will now carry out this program for the two vectors in the problem
(a) If
we sketch 
with its components,
we get:
So 
itself is the
hypotenuse of this right triangle, the x
component is the side of the triangle adjacent to the 50o angle, and the
y component is the side of the triangle opposite the 50o angle. That
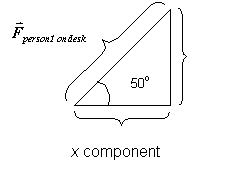means:
cosine50o = 
That is, x component (35 N)(0.64) = 22.5 N and since it points to the right on our axes, it is positive. (On our axis, right is positive and left is negative for x, up is positive and down is negative for y.) The y component is obtained from:
sine50o = 
giving y component = (35 N)(0.77) = 26.8 N
This
component points upward so it is positive also. We now have the x and y components of 
. They are:
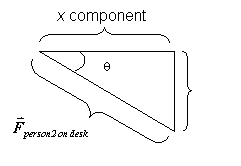
In a similar way we find the components of
. Here we have a
preliminary step
we have to complete; we have to find the angle
q. The angle we were given was 340o, which
means q = 360o – 340o = 20o. Now we
proceed in
the same way we did with 
cosine20o
= 
x component = (27 N)
cosine 20o = 25.4 N
and this will be positive since it points to the right.
y component = (27 N) sin 20o = 9.2 N
but this will be negative since it points down. The components of
are: F(2)x = +25.4 N and F(2)y =
-9.2 N
b) In this step we add the components independently. (Why can we do this?) In other words, we find the x component of the resultant from
Fx = F (1) x + F (2) x = +22.5 N + 25.4 N = 47.9 N
and the y component from
Fy = F (1) y + F (2) y = +26.8 N – 9.2 N = 17.6 N
c) Finally, we “sum” the two components of the resultant using the Pythagorean theorem, and then determine the angle for the resultant. First, we get the magnitude of the resultant
Now the angle can be found using either the sine, cosine, or tangent.
Note that this means 20.17o above the x axis (i.e., in the first quadrant) since Fx and Fy are both positive. (What quadrant would the angle be in if Fx was negative and Fy positive? What about if Fx and Fy were both negative?)