Physics Department [Return to Examples]
KINEMATICS EXAMPLE 10
A 65 kg shot putter gets frustrated and throws a 5 kg shot put off a 20 m cliff. Because of her frustration, she manages to throw the shot put at a 35o angle at 8 m/s, although 7.4 m/s was her previous best throw. How far from the base of the cliff will the shot put land?
Given: Mass of shot putter → 
; mass of the shot put → 
; height of the cliff
→ 
; angle of throw (=
direction of initial velocity) →
(assumed to be above
the horizontal); initial speed →
; previous best initial speed → 
implicit given is the
acceleration due to gravity 
downward (i.e.,
points toward the center of the earth).
Unknown: Horizontal distance from base of cliff to point where the shot put lands
→ 
Physical Situation Physics Sketch
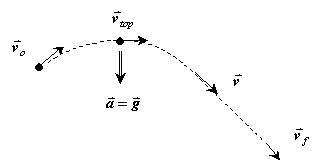
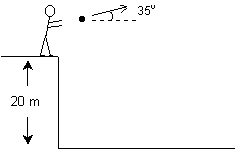
Physical Principles and/or Ideas: projectile motion, which means we need the ideas for constant velocity motion and for constant acceleration motion.
In real problems, one of the integral, and often very difficult, parts of the process is determining what information is relevant and what information is irrelevant. This problem contains irrelevant information. How do we figure out what items are irrelevant? One of the easiest, and most effective ways to do this is to determine what the nature of the physical system is and how it is behaving. This is related to, in some cases equivalent to, identifying the relevant physical principle(s). Recognizing that the shot put is going to undergo projectile motion is the key in this problem. Since the shot put is the object we are interested in, the mass of the shot putter is irrelevant. Since the shot put is undergoing projectile motion on the Earth, its mass is irrelevant. (Why is this?) And finally, how fast the shot putter throws the putt at other times is not of concern here.
Solution: We are looking for the horizontal distance, which we could get by multiplying the (constant) horizontal speed by the time the shot put is in the air. The horizontal speed is easily found (it is the magnitude of the horizontal component of the initial velocity, i.e., 8 m/s times the cosine of 35o), but finding how long the shot put is in the air is not so straightforward. Thus, our problem becomes one of finding the time it takes the shot put to reach the ground. How do we find this time?
There are several ways to find the time, differing in how the motion is subdivided. For example, we could think of the motion as having two parts: from being thrown to the top, and then from the top of its path to the ground. However, this time let us think of the motion as having three parts: from being thrown to the top of the path, from the top of the path down to the cliff height, and finally from the cliff height to the ground. Throughout, the horizontal component of the motion is constant velocity motion, while the vertical component is constant acceleration motion. For the time being, we will ignore the horizontal component.
For the first part of the motion, the acceleration and the vertical component of the velocity point in opposite directions. As a consequence, the vertical speed decreases to zero at the top of the path. In fact, that defines the top of the path, the point where the projectile has stopped going up, but has not started to fall yet. (This happens at an instant, so it is not usually observable.) So, for the vertical motion for this part, the shot starts with an initial upward velocity and slows down until it stops (at an instant).
Now we are at a point where we can use an equation; the one we want is
(In this
equation, we have included y subscripts and superscripts to emphasize
the fact that we are only concerned with vertical motion here.) The values we are going to put into this
equation are: 
(remember the
shot-putt’s vertical motion stops, at an instant, at the top), 
(minus because it
points in the opposite direction to the vertical velocity, which we are taking
as positive during the first part of the motion), and 
We label the time as
because all we are
finding right now is the time to the top.
Putting these values into the equation and solving for 
we get:
Now we turn
to the second part of the motion: from
the top of the path back down to the cliff height. The vertical motion for this part is the “reverse” of the first
part. The difference is that for this
part of the motion the acceleration and vertical velocity are in the same
direction, so the vertical velocity will increase back to its initial value,
i.e., 4.59 m/s. This requires the same
time as the trip up, i.e., 
Finally, in the third part of the motion, the vertical component motion is a constant acceleration motion in a straight line starting with a speed of 4.59 m/s and covering a distance of 20 m. For the motion, we use the equation:
The values
we are going to put into the equation are:
(we are going to take
the top of the cliff as the starting point), 
and 
We are now taking
the downward direction as positive.
Putting these in we get:
Solving this quadratic equation, we get 
Since a negative
time has no physical meaning, the answer we want is 
Now we are ready to find the total time. We simply add up the times for the three parts of the motion. We get:
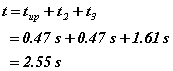
We are now in a position to answer the original question. Way back when we started on the solution, we said the distance could be found by multiplying the constant horizontal velocity by the time in the air, that is:
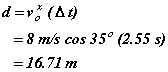
There are other aspects of the situation we could determine:
1) What is the maximum height reached by the shot put?
2) How fast is the shot put going just before hitting the ground?
3) How fast is the shot put going at the top of its path?
4) If she had dropped the shot put, how long would it have taken to hit the ground at the base of the cliff?
What aspects can you think of to determine?