KINEMATICS  EXAMPLE   2

Luke Skywalker’s air car is moving with a velocity of 28 m/s NW.  There is a strong wind blowing 9 m/s SW.  What is Luke’s velocity relative to the ground?

Given:  velocity of air car  = 28 m/s NW and velocity of the wind,  = 9 m/s SW.

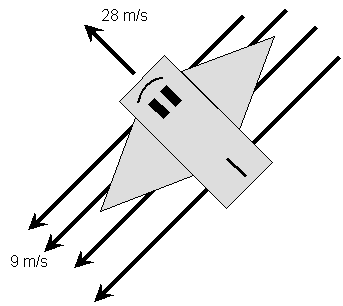(The NW and SW mean 45^o between N and W, and S and W, since no angle is specified).

 

 

                                                                                                                                                           

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

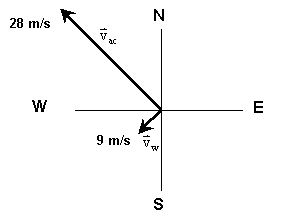
Unknown:  velocity of car relative to the ground,  = ? m/s?

 

Physical Principles and/or ideas:  Vector addition of two vectors at right angles to each

other, Pythagorean Theorem.

 

Solution:         The velocity Luke reads in his vehicle is measured relative to the medium he is traveling through, the air.  But in this case, the air is moving also, so Luke’s velocity relative to the ground is the vector sum of these two velocities.  A vector sum means taking into account both the magnitudes and the directions of the vectors.

We can see what we need to do

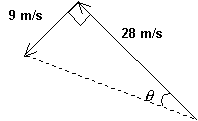in the figure on the right.

 

                        The dashed line, which is the

                        hypotenuse of the right triangle,

                        is what we need to find; but we

                        also need to find the angle q

          since our answer is a vector,

                        which means it must have a

                        magnitude and a direction.

We find the magnitude of the resultant in this case by applying the Pythagorean Theorem, since we want the size of the hypotenuse.  We get:

 

 

 m/s = 29.41 m/s

 

Now we know the magnitude of Luke’s velocity, but we do not know what his direction is.  To find the direction we need to determine the angle q.  We can get that by using the cosine function (or we could use the sine, or tangent function).  We find:

 

                        cosine q =

 

                        sine q =

 

                        tangent q =

 

So, we see that all three procedures do indeed give us the same answer.  We now know the angle the resultant velocity makes with the 28 m/s NW vector.  To find the actual direction we can either subtract the 17.8^o from 45^o to get 27.2^o which is North of West, or we can add 17.8^o to 45^o to get 62.8^o which is West of North.  These two angles, 27.2^o N of W and 62.8^o W of N, are compliments of each other so they do represent the same direction.

            So Luke’s velocity relative to the ground is

                                               

Another way to write this would be , this is if we take 0^o as the East (or x) axis and read counterclockwise from there.

 

All problems involving two vectors that are perpendicular to each other, no matter what quantities the vectors represent (displacement, velocity, acceleration, force, momentum, field or others), can be worked this way.

 

What difference would it make in terms of the procedures used to solve this problem if the:

            velocity had been directed SE?

            wind had been directed W?

            object was an airplane?

            two velocities were at a 70^o angle relative to each other?

 

Why would the following NOT be a legitimate way to solve this problem?