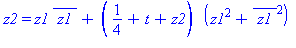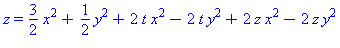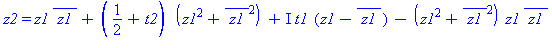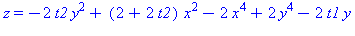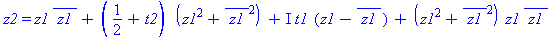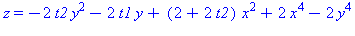| The blue formulas give h(z1), followed by f(x,y) |
|
|
|
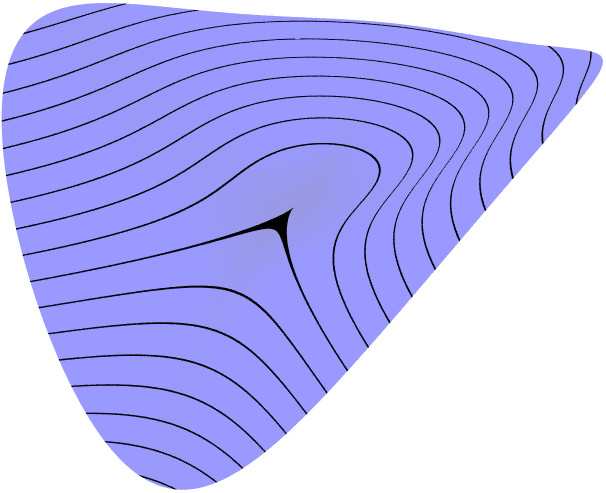
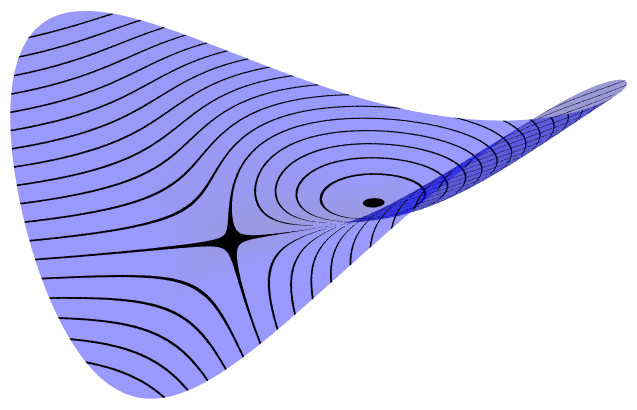
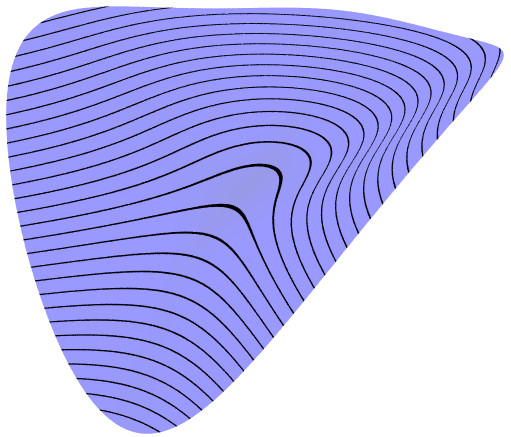
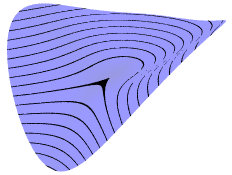
Cubic Parabolic The level set through the
critical point has a cusp shape. This kind of critical point is
"unstable," in the sense that small changes in the function can
result in a surface with different kinds of critical points, as
the following two pictures show.
Maple worksheet
POV scene file
|
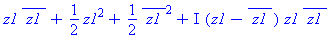 |
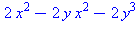 |
| γ = 1/2 |
|
|
|
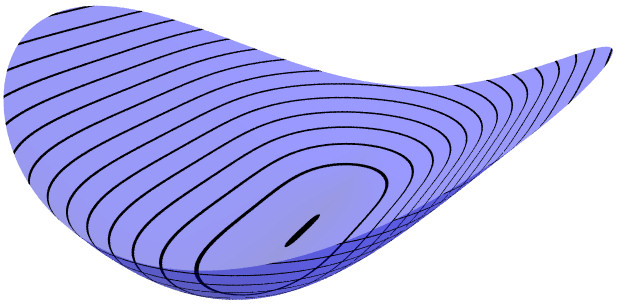
Deformation of Cubic Parabolic into Elliptic/Hyperbolic pair
Adding a linear term with coefficient t < 0 deforms the
surface with an unstable parabolic critical point into a surface
with a pair of stable critical points, one elliptic and one
hyperbolic.
Maple worksheet
POV scene file
|
|
|
|
|
Deformation of Cubic Parabolic into surface without critical
points Using the same formula as above, but with linear
coefficient t >0, results in a surface with no critical
points.
This can be understood as a "cancellation" phenomenon, where
t is a time parameter, and the elliptic/hyperbolic points
move toward each other as t increases, collide at
t=0 to form a parabolic point, and then disappear as
t becomes positive.
Maple worksheet
POV scene file
|
|
There are two types of quartic (degree 4) surfaces with a parabolic critical point;
for lack of better terminology, they are labeled type (I) and type (II). |
|
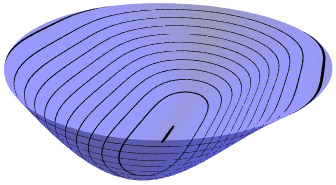
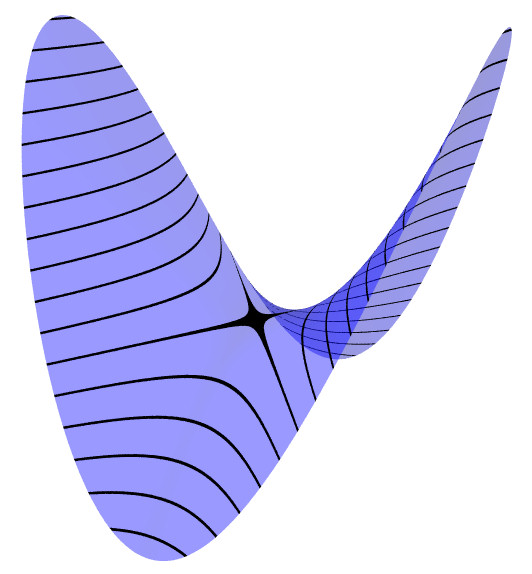
Quartic Parabolic (I) This surface also has a
critical point which is a local minimum. In the picture, the
surface is more flat in the y direction than the x
direction, and the critical point is in the center of the long
black dot. The surface is defined by a quartic (degree 4)
equation and is unstable under deformations, as the following
three pictures show.
Maple worksheet
POV scene file
|
|
|
|

|
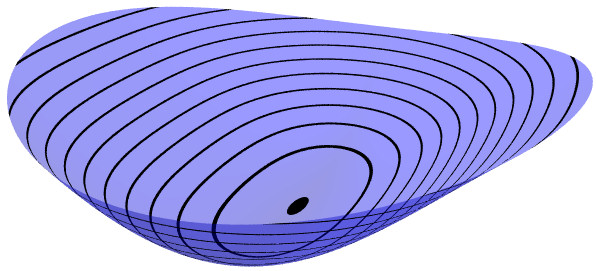
Deformation of Quartic Parabolic (I) into Elliptic
Adding a linear term with coefficient t1 < 0 or t1 > 0
gives a stable elliptic critical point.
Maple worksheet
POV scene file
|
|
|
|
|
Deformation of Quartic Parabolic (I) into Elliptic
Adding quadratic terms with coefficient t2 < 0
also gives a stable elliptic critical point.
Maple worksheet
POV scene file
|
|
|
|

|
Deformation of Quartic Parabolic (I) into two Elliptic + one
Hyperbolic Adding the same quadratic terms with coefficient
t2 > 0 gives three stable critical points.
Maple worksheet
POV scene file
|
|
|
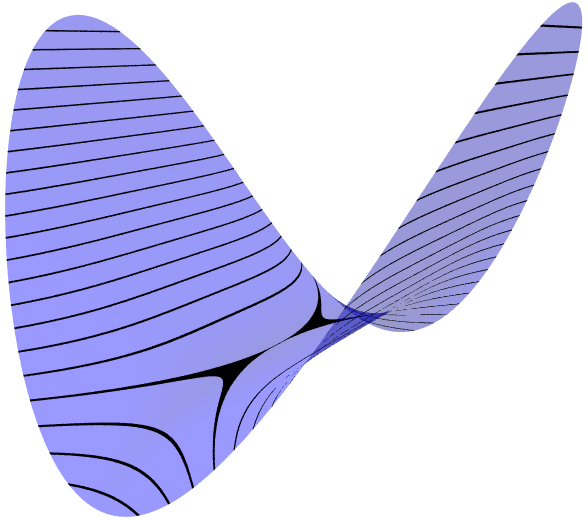
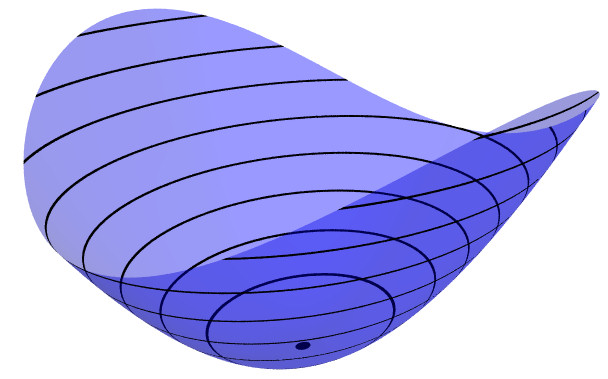
Quartic Parabolic (II) This surface has a critical
point where surface is more flat in the y direction than the
x direction, and the level set through the critical point is a
self-tangent curve, instead of an X shape like the stable saddle
point.
Maple worksheet
POV scene file
|
|
|
|

|
Deformation of Quartic Parabolic (II) into Hyperbolic
Adding a linear term with coefficient t1 < 0 or t1 > 0
gives a stable hyperbolic critical point.
Maple worksheet
POV scene file
|
|
|
|

|
Deformation of Quartic Parabolic (II) into Hyperbolic
Adding quadratic terms with coefficient t2 > 0
also gives a stable hyperbolic critical point.
Maple worksheet
POV scene file
|
|
|
|
|
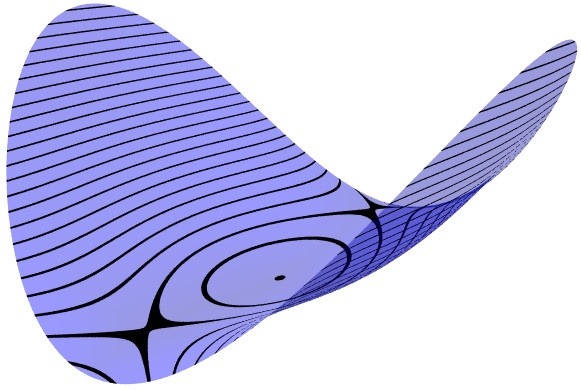
Deformation of Quartic Parabolic (II) into two Hyperbolic + one Elliptic
Adding the same quadratic terms with coefficient
t2 < 0 gives three stable critical points.
Maple worksheet
POV scene file
|
|
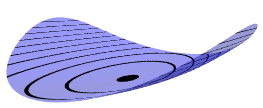
AnimationsClick on the small image to see an animation |
 150KB
gif 150KB
gif
POV scene file
POV ini file
|
A surface with an elliptic point, γ = 1/4, can be deformed using
a time parameter t, by replacing γ with γ +
t, and the surface will still be elliptic for t close to
0. In the animation, t varies between -0.2 and +0.2, so the
coefficient γ varies between 0.05 (almost circular cross
sections) to 0.45 (almost a parabolic cylinder). The (black) level
curves are always ellipses although this implicit equation also has
some cubic terms. The "deflating ellipsoid" animation on the graphics
gallery page also demonstrates this type of deformation.
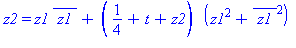
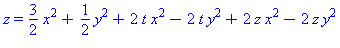
|
|
 250KB
gif 250KB
gif
POV scene file
POV ini file
|
This is the deformation of a cubic parabolic point, as described
above, so sometimes there is a pair of critical points, and sometimes
there is no critical point.
|
|
 596KB
gif 596KB
gif
POV scene file
POV ini file
|
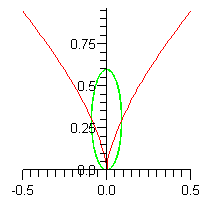
This is a deformation of the quartic parabolic point, Type I, as
described above. There is a two-dimensional parameter space
(coordinates t1, t2), so to get an animation depending
on the time parameter T only, let t1, t2 follow
an elliptical path (green) in the parameter space, so that at the
start time T=0, the parameters are at the origin, so the
surface has the quartic parabolic normal form. As time passes, the
parameters move around the ellipse - when (t1, t2) is
below the (red) discriminant curve, the surface has exactly one
elliptic point, when (t1, t2) is a point on the curve
but not at the cusp, the surface has an elliptic point and a cubic
parabolic point, and when (t1, t2) is a point above the
curve, the surface has two elliptic points and one hyperbolic point.
|
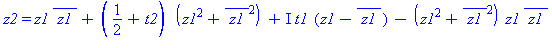
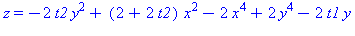
|
|

 318KB
gif 318KB
gif
POV scene file
POV ini file
|
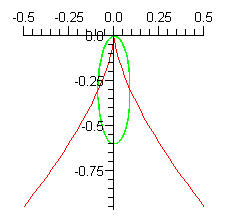
This is a deformation of the quartic parabolic point, Type II, as
described above. There is a two-dimensional parameter space
(coordinates t1, t2), so to get an animation depending
on the time parameter T only, let t1, t2 follow
an elliptical path (green) in the parameter space, so that at the start time
T=0, the parameters are at the origin, so the surface has the
quartic parabolic normal form. As time passes, the parameters move
around the ellipse - when (t1, t2) is above the (red)
discriminant curve, the surface has exactly one hyperbolic point, when
(t1, t2) is a point on the curve but not at the cusp,
the surface has a hyperbolic point and a cubic parabolic point, and
when (t1, t2) is a point below the curve, the surface
has two hyperbolic points and one elliptic point.
|
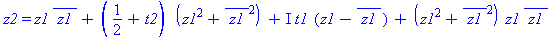
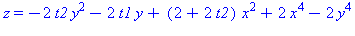
|
|











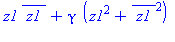
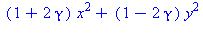
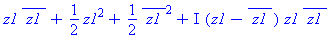
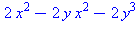
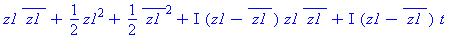
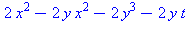
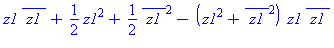
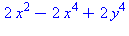
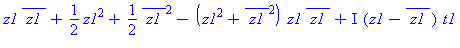
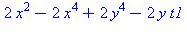
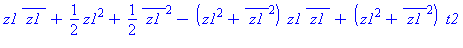
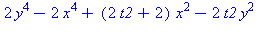
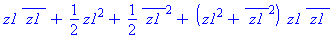
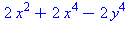
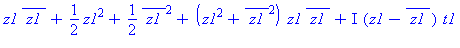
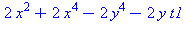
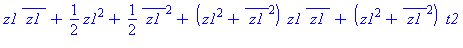
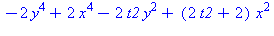

 150KB
gif
150KB
gif