MA 16600  Analytical Geometry & Calculus II
Recursive Sequences

The current activity is a lesson using graphing calculators to explore various initial seeds for the recursive sequences a_n  = 1 +  a_n-1 /2 and  a_n  = 25 −  66/a_n-1 . This activity provides a natural hook to entice students to question how the choice of the seed a₀  affects the limit. For the first sequence, every seed produces the same limit, which in this case, is a unique value since the limit L is the solution to L = 1 + L/2 which, by graphical analysis, they can see has one solution. However, the second sequence can converge to 22 or 3, as shown in the lesson. These are the only two solutions to L = 25 − 66/L. The solutions are called fixed points.  A seed of a₀ = 3 produces the limit 3, but other than 3 or 0, no matter what seed a₀ they try with their graphing calculator, the sequence will converge to 22. (They don't know this for a fact yet. Read on.) I show the intersection of the graphs of f(x) =  25 − 66/x and y = x and use a cobweb plot to follow the trail to the fixed points.
I will revise the activity with an out-of-class exploration with their graphing calculator and generative AI as follows:
a.  i. Enter the seed a₀ = 1 in your graphing calculator for the sequence a_n = (a_n-1−3)². What happens?
ii. Enter the seed a₀ = 4 in your graphing calculator. What happens?
iii. Explore these two seeds with this cobweb plot. Use the slider to find any additional seeds that behave in a similar fashion to 1 and 4.
iv. What happens if you enter seeds other than 1, 4 and those listed in part a.iii? 
v. Ask generative AI, is there any initial seed that would make a_n = (a_n-1 −3)² converge?
b. Determine if there is a nonzero seed a₀ ≠ 3 that yields the limit 3 for the sequence a_n =25 − 66/a_n-1 . If no such seed exists, explain why not. 
c. Formulate targeted questions to generative AI to construct a recursive sequence which has more than 1 limit and specify at least two seeds that will enable convergence to each of the limits, where the seed is different than the limit itself.  No student may submit the same formula. Save your chat and submit it in this assignment. If generative AI produces errors, be sure to let it know when interacting with it so that it can self-correct. Use graphing software to produce graphs of y = x and your formula f(x).
--------------------------------
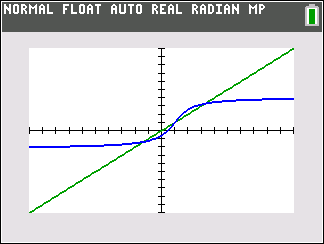
Pedagogical Objectives: By asking the question in part a, the graphing calculator will show that for a₀ = 1 and 4 the sequence diverges by oscillation. The cobweb plot will show that 2 and 5 also diverge by oscillation. For other seeds, the sequence diverges to ∞ .  Generative AI will share with students no seed will result in convergence for the sequence in part a and discuss the stability of fixed points and the property that if L is a fixed point and  | f ' (L) | < 1, which is the slope of y = x, then L is stable.  Generative AI will guide students in part b to see that no such seed other than 3 exists for which a_n =25 − 66/a_n-1  converges to 3, since, for f(x) = 25− 66/x, we have f '(3) > 1. Any cobweb plot will never reach 3 because the slope of the curve at (3, f(3)) exceeds the slope of y = x. In part c, it will be very difficult for generative AI to construct a function which intersects y = x multiple times at values where the slope of f(x) is less than 1. Students will need to correct AI.  However, students may find that interacting with generative AI can help them create such a function by finding what types of functions fail. One such possibility is f(x) = 2arctan(x-1)+1, which has three fixed points and this cobweb plot.

I have put the following on my syllabus. (I also repeat these tips and the tips below in multiple places in the course: at the portal to My Math Lab in Brightspace, on the My Math Lab Home page itself, in a syllabus scavenger hunt, and in the above assignment.)

What is the best way to use Artificial Intelligence (AI) as a student in this class? Consider these tips from ChatGPT.
 
Use AI and My Math Lab (MML) to help you learn rather than just earn points. For more, watch this 2 minute movie clip (a silent movie) and check out these tips.

Generative AI is trained to deliver a response with the shortest wait time possible. This may cause it to apply procedures you have not yet learned, omit steps altogether, or provide incorrect answers. AI may make up fictional answers just to shut you up. It will deliver rubbish to you as if it is absolute truth. A healthy distrust is appropriate. To coach AI, use these prompts:

• “Hey, slow down, check your results by using Python, and solve the problem step by step.”
• Whenever AI skips a step, it is more likely at that point that is delivering rubbish. Ask AI to tell you to fill in the missing steps. Tell them your grade level. “Drop down a notch, Einstein. Teach a first-year college student how to solve the problem step by step.” or “I haven’t learned that method yet. Tell me another way to solve it.”
• AI perceives emotion. It performs better if you say “It’s vital to me you get it correct and that it makes sense to me. My life depends on this.”

Generative AI might be used effectively to:

• help you learn a difficult concept. “Don’t give me solutions, but just give me help along the way”, i.e., like here (with Khan Academy) and here (with ChatGPT-4o developers). This will lower the chance you will get rubbish.
  Fun Fact: Machine learning uses a gradient descent algorithm (similar to Newton’s method from Calculus 1 in multiple dimensions using linear algebra with discrete data) which produces best results if you ask it to show steps.
• tell you how a concept might be important for your career path.
• create example quiz questions. “In terms of difficulty, on a scale of mild, medium, or spicy, make it <choose a level>.”
• tell you the best ways to study for an exam. 

At present, generative AI might not do very well with the following; however, in class I can show you how to:

• validate if your answer is correct or share how you can use other strategies to know if your answer is correct.
• critique if your solution is the best one possible or share if there is a more efficient or better approach.

No need to pay additional $: While Wolfram Alpha, Chegg’s Mathway, or other computer algebra systems are more robust than the current state of generative AI, there is often a paywall for these to explain the steps to the solution process. Do not pay. Instead, I recommend Pearson’s interactive AI-powered study tool newly launched this fall. While not flawless, this AI Tutor will draw from our textbook’s solution manual to more accurately guide you on your journey to understanding. It may be helpful to know another resource provided to Purdue students at no additional cost: Microsoft Copilot with Data Protection, available at copilot.microsoft.com/. To access Copilot, sign in with your PFW account credentials.