
This surface is the rotationally symmetric case, where C is on L. When the radius is c = 1, the equation is
It is equal to the surface of revolution generated by rotating the parabola x = (z2 - 1)/2 around the z-axis.

The horizontal cross-sections (by planes perpendicular to L) are ellipses, all with the same eccentricity (except at the singular points). Each cross-section by a plane containing L is a union of two parabolas.

The horizontal cross-sections are parabolas (except at the plane through the origin). Each cross-section by a plane containing L is a union of two parabolas tangent to L at the origin (except the plane containing C, which intersects the surface along the double line and one parabola).
There are some solutions of the implicit equation which are not solutions of the equation b = |a - c|. Points on the negative x-axis (where the surface crosses itself) are equidistant from L and S, as are points on the line segment connecting the origin (0,0,0) to the center C = (1,0,0). However, points of the form (x,0,0), with x > 1, satisfy z4 - 4xz2 - 4y2 = 0, but are not equidistant from L and S.
The shape can be parametrized by quadratic polynomials: x=u2-v2, y=2uv, z=2u, so it is a Steiner surface (of Type 4) and also falls into a classification of quadratically parametrized affine surfaces.
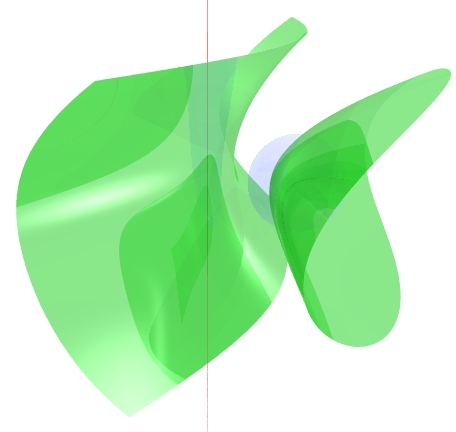
The left half of the surface is the locus of equidistant points, which all lie outside the sphere, so the equation is b = a - c. Each of its horizontal cross-sections is one branch of a hyperbola.
The constant c appearing in the implicit equation

The second case is where c=0 and C=(0,0,0). The locus of points equidistant from L and S is the xy-plane, z = 0 (light green).
