Packing Ellipsoids
Oct. 27, 2004 talk for the PI Math Club
Filling space with solid shapes
Polyhedra:
| Newton-Gregory problem - 1694-1953:
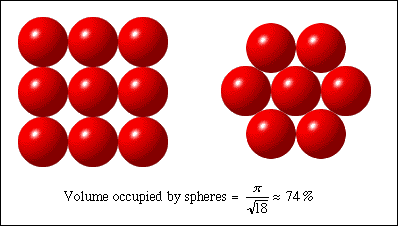
Maximum number of contacts for spheres = 12 Kepler problem - 1611-1998: Sphere packing - also with 12 contacts The most efficient sphere packing (two views):
Experimental average # of contacts in a random sphere packing: 6.4. Experimental packing efficiency in a random sphere packing: approx. 64%. |
Demonstrating circular disk packing.
Most efficient packing: hexagonal array, approx. 90.7% area coverage. |
| Photos from the PI Math Club talk on random packing of ellipsoids |
|
| Audience Participation | |
 |
|
| The ellipsoids at the bottom of the container are not randomly packed | |
| Measuring the volume of 100
ellipsoids using the water displacement method of Archimedes, with the assistance of PI Math Club V.P. K. Boyd The experimental conclusion: 68 cubic centimeters, or an average of
0.68 cc each. |
|
| 4000 ellipsoids sorted into bags of 1000 | |
| Pouring into a 5000 cubic centimeter container | |
| The first 1000 | The next 1000 |
| The next 1000 | The next 1000 |
| The conclusion: it takes about 5200 ellipsoids to fill the 5000 ml container. | |
| The calculations:
Using our estimate of the volume of an individual ellipsoid, Using the value of 0.636 cc for the individual volume found in the research papers, Either way, we get a higher packing density than the experimentally measured This confirms recent experiments and simulations with randomly packed ellipsoids.
(see news articles, below) |
|
| After 24 hours in the Math Department TeaRoom. | After 48 hours. |
Princeton lab web site
Ellipsoids in the news:
Science Magazine summary (PDF)
Another Container Shape.
Prof. Coffman's web site
on Linear systems of
ellipsoids
- possibly applicable to the
"collision detection" problem for computer simulation of ellipsoid
packing
Thanks to the IPFW Department of Chemistry for a loan of equipment
Backto Professor Adam Coffman's home page.