Dynamics Example 2 © 2000 D.P. Maloney

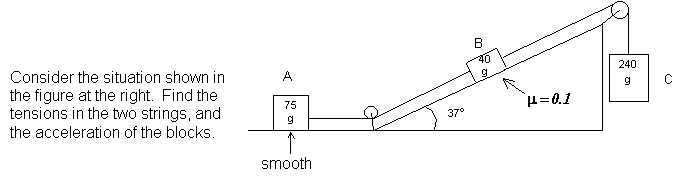
Physical Situation: Given in the figure above.

Physics Sketch: Here we have three, a free-body diagram for each block.

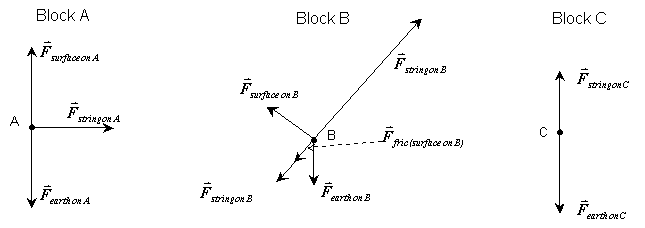
Solution: We are looking for three things in this problem. In algebra, we learned that we need to have three equations to find three unknowns. Where do we get these equations? They come from applying Newton’s second law to each of the three blocks. The second law says we take the vector sum of the forces acting on the object and set that equal to the product of the object’s mass and acceleration.

Before we actually apply Newton’s second law to each block, notice that two of the blocks are on surfaces. They are not going to accelerate, or even move, up off of the surface, nor down into the surface. They will move along the surfaces; that (the fact that the acceleration is zero) means the forces perpendicular to the surfaces sum to zero for each block. All we need to worry about are the forces that are parallel to the surfaces, and we can treat their directions as either positive or negative. Looking at the physical situation, we expect the 240 g block to “fall” and the other two to move up the incline for the 40 g block and to the right for the 75 g block. Working from this expectation, we will take forces that make the blocks accelerate in these directions as positive, and forces pointing opposite to the assumed acceleration as negative.

Let’s start with block A. The gravitational force (earth on A) and the normal force exerted by the surface (surface on A) sum to zero, as we pointed out above. Since this surface is smooth, there is no frictional force. So the only force, parallel to the surface, which acts on A is that exerted by the string. We will call this (T for tension). So applying Newton’s second law we equate this force to the product of block A’s mass and acceleration. That is,

This gives us our first equation.

Let’s consider block C next. The free-body diagram shows only two forces acting on C, one is the gravitational force (earth on C) and the other is the force exerted by the string. In drawing the free body diagram, we have incorporated our inference that C will “fall”. How did we do this? By making the gravitational force longer than the force exerted by the string, we included our expectation about which way C will accelerate. Applying Newton’s second law to block C, we get:

This is our second equation.

Before we move on to block B, there are several points about the equation we just derived that merit attention. First, notice that the tension here is labeled to distinguish it from . There are two strings so there are two different tensions. Second, since the gravitational force and the tension point in opposite directions we subtract the tension from the gravitational force. Third, we can rewrite the gravitational force, , as . So our equation becomes:

Finally, we turn our attention to block B. Before we apply Newton’s second law, we need to break the gravitational force into components. The components that are useful here are one perpendicular to the incline surface and one parallel to it. These are useful because the one perpendicular to the surface will “cancel” the normal force exerted by the surface, and the one parallel to the surface can be readily combined with the other forces acting on B. How do we determine these components?

Getting these components requires some geometry. First, let’s draw the outline of the incline and put the gravitational force on the diagram.

The gravitational force on an object always points toward the center of the earth, which means it is perpendicular to the surface of the earth. Since the base of the incline sits on the surface (or on something like a table which will be parallel to the surface), the gravitational force is perpendicular to the base of the incline. Now we construct a right triangle with our gravitational force vector as the hypotenuse, one side parallel to the surface of the incline, and the other side perpendicular to the incline surface. This diagram is shown below, where we see we have two right triangles that appear to be similar.

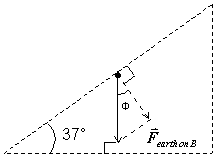
Notice that the two sides of the force triangle that form the angle Φ are perpendicular, separately, to the two sides of the incline that form the 37° angle. There is a theorem of geometry which allows us to conclude from this pair-wise perpendicular situation that the angle Φ = 37°. So the component of the gravitational force that is parallel to the incline surface is , and the component perpendicular to the incline surface is . Now we can return to applying Newton’s second law to block B.

The component of the gravitational force which acts parallel to the incline surface points “down” the incline, as do the frictional force exerted by the surface and acting on B. The only force that points “up” the incline is on B. So our equation becomes:

But the frictional force is given by the product of the coefficient of friction and the normal force. Here the magnitude of the normal force is . So the magnitude of the frictional force is and our equation becomes:

We have arrived at the point where we have our three equations for the three unknowns. For clarity, we rewrite the three equations here:

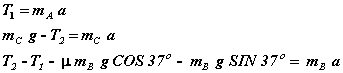
We will solve these using the substitution method. Solve the second equation for , and then substitute the expressions for and into the third equation.

Isolating the acceleration, we get:

Plugging in the values we know gives:

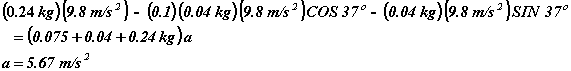
Putting this value back into the equation for block A, we get:

In a similar way using the equation for block C, we get:

Once we have found numerical values for our unknowns, we should think about whether the values found are reasonable. One way to do this is to check that a value lies between “extreme” values. For example, if the blocks did not move, the acceleration would be zero, and if block C fell unhindered, its acceleration would be 9.8 m/s², our acceleration value of 5.67 m/s² lies between these “extremes”. Another way to check on values is to see that the system “works” as expected with the values found. For example, we found that the magnitude of is greater than the magnitude of and that is necessary if block B is going to accelerate up the incline.