MA 15400 Course Assignments
Fall 2019

 

Class meeting Topic Assignment


Monday,
August 26

 

 Section 7.1
Periodic Functions		 Welcome to our class. Check out the schedule for Welcome Week.

Handouts: Ferris Wheel  (See pictures of the London Eye: 1  2 3)
                Syllabus
                Practice Questions to Check Prerequisite Skills Needed for MA 15400

Today's objectives:
 1. Identify if a graph represents a periodic function.
 2. Determine period, amplitude and midline.
 3. Use a graph to find and interpret y if given t or vice versa.

Due: Wednesday, August 28
Read: General Course Information, the Syllabus, and, if you have the text, Section 7.1 and 7.2
Do:    If necessary, purchase a TI-84 Plus CE or equivalent and purchase eHW access.
           Note: access is good for one year.
           Practice on eHW Flash Cards: 7.1 Periodic Functions.
           Optional: Section 7.1 -- your choice of 1-17, 23-34 as needed.
           Review eHW Math Background Needed for MA 15400 and eHW Flash Cards for Prerequisite Skills 
           See also Practice Questions to Check Prerequisite Skills Needed for MA 15400 and these Worked out Solutions.
           You should also be proficient in these skills needed for MA 15300.

Prepare for QUIZ 1 next Wednesday, Sept 4 over prerequisite skills. (See green packet and eHW.)

Due Friday, August 30, 11:59 pm: E-HW: Quiz on John's Syllabus- Score 90% or Higher by the Deadline!
Note: You need to get a score of 90% or higher for this eHW by the deadline to open up any future eHW assignments.
You have unlimited attempts.

Due Tuesday, Sept 3, 11:59 pm:  E-HW: Math Background Needed for MA 15400
Due Tuesday, Sept 3, 11:59 pm:  E-HW0: General Course Information and Using eHW

Wednesday,
August 28		 Section 7.2
The Sine Function
(and its Sidekick, Cosine)
Today's objectives:
  1. Sketch the position of a point on a circle of radius r corresponding to a given angle (or value of time or number of revolutions) and give its coordinates
  2. Find angles between 0° and 360° which have the same sine or cosine of a given angle.
    Determine in which quadrant an angle lies if given certain conditions.

    Do (for practice): 
    Flash Card     7.2 Report the coordinates of a point on a circle of radius r given the angle.
    Flash Card     7.2 Use the definitions of sine and cosine
    If you have a text, see read Section     7.3 and do Section 7.2 -- 1, 3, 5-31
Click on the photo to enlarge (and download for printing).

Prepare for QUIZ 1 next Wednesday, Sept 4 over prerequisite skills.
(See the green packet with KEY and eHW Flash Cards for practice.)

Due Friday, August 30, 11:59 pm: E-HW: Quiz on John's Syllabus- Score 90% or Higher by the Deadline!
Note: You need to get a score of 90% or higher for this eHW by the deadline to open up any future eHW assignments.
You have unlimited attempts.

Due Tuesday, Sept 3, 11:59 pm:  E-HW: Math Background Needed for MA 15400
Due Tuesday, Sept 3, 11:59 pm:  E-HW0: General Course Information and Using eHW  
Friday
August 30		 Section 7.3
Radians
Today's objectives:
  1. Convert an angle from degrees to radians and vice versa.
  2. Interpret the radian measure of the central angle of a circle of radius r as the number of radius lengths, r, that you need to wrap around the rim of the circle on the arc spanned by the angle.
  3. Understand the relationship between arc length, radius and an angle measure in radians.
    If given two of the arc length s, radius r, or an angle θ, find the third.
The radian measure of an angle θ is the number of radius lengths that a bug would walk on the rim of a circle spanned by the angle.
For a circle of radius r, if s is the arc length the bug walks on the rim, then we have
s = (the radius r) x (# of radius lengths) or
s =  r x θ

Here is a short video of the bug taking a tour around the rim of a circle,
counting radius lengths as he goes. It is a silent movie since bugs can't talk.

Suppose a central angle θ  in a circle of radius r spans an arc of length s. Measure how many radius lengths that the length of the arc is.  This number of radius lengths is the radian measure of the angle θ: we have rθ = s.

Do (for practice): 
Flash Card 7.3 Find points on a circle using radian measure of quadrantals
Flash Card 7.3 Radian Measure as Number of Radius Lengths Around a Circle
If you have a text, read Chapter 7 Skills Refresher, see Section 7.3 -- 1-56 as desired (for practice).

Prepare for QUIZ 1 next Wednesday, Sept 4 over prerequisite skills.
(See the green packet with KEY and eHW Flash Cards for practice.)

Due Tuesday, Sept 3, 11:59 pm:  E-HW: Math Background Needed for MA 15400
Due Tuesday, Sept 3, 11:59 pm:  E-HW0: General Course Information and Using eHW  
Due Friday, Sept. 6, 11:59 pm: E-HW 01 Sections 7.1 - 7.2
Due Wednesday, Sept. 11, 11:59 pm: E-HW 01 Sections 7.3
Class meeting Topic Assignment
Mon, Sept. 2 Labor day holiday No class meeting
Wed., Sept. 4 Chapter 7 Skills Refresher
Special Angles		 Today:  QUIZ 1 over Prerequisites. We briefly looked at special angles

Do (for practice): 
Flash Card Ch 7 Skills Refresher Properties of Special Triangles
Flash Card Ch 7 Skills Refresher Exact Values of Sine and Cosine

If you have a text, see Chapter 7 Skills Refresher (page 325) -- 25-30

Due Friday, Sept. 6, 11:59 pm: E-HW 01 Sections 7.1 - 7.2
Due Wednesday, Sept. 11, 11:59 pm: E-HW 02 Sections 7.3
Due Friday, Sept. 13: Writing Assignment 1: Bug on a Square Track
For next class, Fri., Sept. 6, please come prepared with the first two pages of WR1 completed.

Fri., Sept. 6 Chapter 7 Skills Refresher
Special Angles cont'd		 Today's objectives:
1. Find exact values of sine and cosine for multiples of 30°, 45°, and 60° or their radian equivalents π/6, π /4, or π /3.
2. Use proportional reasoning to find sides of special triangles.

Do (for practice):
Flash Card Ch 7 Skills Refresher Properties of Special Triangles
Flash Card Ch 7 Skills Refresher Exact Values of Sine and Cosine
If you have a text, see Chapter 7 Skills Refresher  (page 324) -- 1 - 24, 26-31 

Due tonight, Friday, Sept. 6, 11:59 pm: E-HW 01 Sections 7.1 - 7.2
Due Wednesday, Sept. 11, 11:59 pm: E-HW 02 Sections 7.3
Due Friday, Sept. 13, 11:59 pm: E-HW 03 Chapter 7 Skills Refresher
Due Friday, Sept. 13: Writing Assignment 1: Bug on a Square Track

Prepare for QUIZ 2 next Monday, Sept. 9 over 7.1 and 7.2
Class meetingg Topic Assignment
Mon, Sept. 9 Section 7.4
Graphs of the Sine and Cosine (and Outside Changes to the Formula)		 Today:  QUIZ 2 over 7.1 and 7.2
We explored the graph of y = Asin(x) + k (Outside additive and multiplicative changes)

Today's objectives:
1. Solve simple trig equations over a requested interval; for example on the interval [0, 2π) find θ if sin θ = 1/2, providing exact values of angles measured in radians when they are multiples of π/6, π /4, or π /3. Be aware of when more than one solution exists! Be able to sketch the angle or angles.
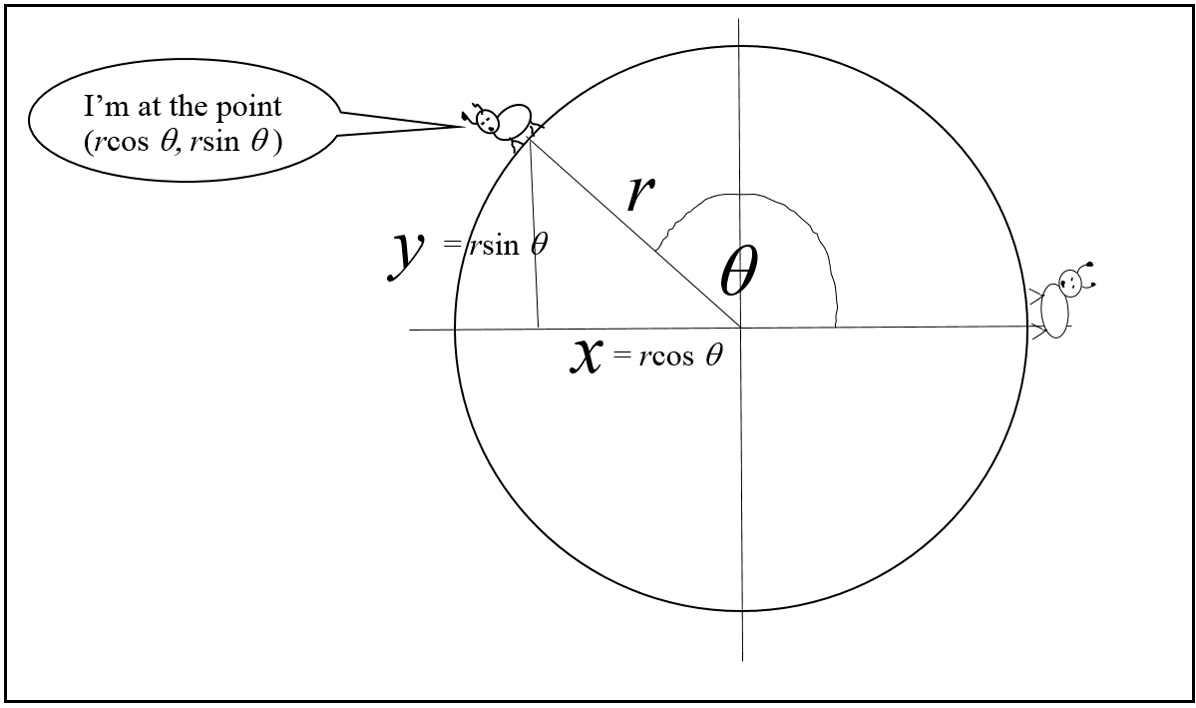
2. Know the main characteristics (period, amplitude, midline, domain, range, odd/even symmetry, when it is positive, negative, increasing, decreasing, if it starts at or above the midline) of the graph of y = sin θ, and y = cos θ. Relate this to the unit circle as the x-coordinate (cosine) or the y-coordinate (sine) of the point on the circle.
3. For y = Asin(x) + k or y = Acos(x) + k , identify the period, amplitude, and midline.

We discussed the domain, range, period, and amplitude of y = sin(x) and y = cos(x) and how these can be determined from the unit circle.
We looked at an outside change to the function, which results in the original function being transformed vertically (change to the output).

  1. y = Asin(x) and y = Acos(x) have amplitude |A|. 
    For A > 0, 
    the graph of y = Asin(x) vertically stretches or compresses the graph of  y = sin(x) by A units.
    the graph of y = –Asin(x) is a vertical reflection of the graph of y = Asin(x).
    Similarly for y = cos(x).  
     

  2. y = sin(x) + k and y = cos(x) + k have midline k.
    For k > 0, 
    the graph of y = sin(x) + k vertically shifts the graph of y = sin(x) up k units.
    the graph of y = sin(x) – k vertically shifts the graph of y = sin(x) down k units.
    Similarly for y = cos(x).  

The first multiplies the output by a quantity; the second adds/subtracts a quantity to the output.

Do (for practice):
Flash Card 7.4 Period, Amplitude, Midline
If you have a text, see Section 7.4 -- 1-24, 26-30, 34-38

Due Wednesday, Sept. 11, 11:59 pm: E-HW 02 Sections 7.3
Due Friday, Sept. 13, 11:59 pm: E-HW 03 Chapter 7 Skills Refresher
Due Friday, Sept. 13: Writing Assignment 1: Bug on a Square Track
Due Monday, Sept. 16: Writing Assignment 2: What's My Angle?
Wed., Sept. 11  

Section 7.5
The graph of
y = sin(Bx)
(Inside multiplicative change)

 For the function y = AsinBx + k
we explored the effects of  B on the period to find that,
for positive values of B, this graph has a period of  2π/B, an amplitude of  |A|, and midline which is y = k.

 Do (for practice):
Flash Card 7.4 Period, Amplitude, Midline
 Flash Card 7.5 Find a Formula of a Sine or Cosine Function (No Phase Shift Needed)
Flash Card 7.5 7.5 Find a Formula of a Sine or Cosine Function (Ferris Wheel)
 If you have a text, see Section 7.5 -- 1-12, 21-26

Due tonight, Wednesday, Sept. 11, 11:59 pm: E-HW 02 Sections 7.3
Friday, Sept. 13: QUIZ 3 over 7.3 and Chapter 7 Skills Refresher

Due Friday, Sept. 13, 11:59 pm: E-HW 03 Chapter 7 Skills Refresher
Due Friday, Sept. 13: Writing Assignment 1: Bug on a Square Track
Due Monday, Sept. 16: Writing Assignment 2: What's My Angle?
Fri., Sept. 13  

 

  

This page is on the Web at http://users.pfw.edu/lamaster/ma154/f19ma154.htm