The Hippopede of Proclus

Consider a torus, T, as a surface of revolution, generated by a circle with radius r > 0, and with center at distance R > 0 from the axis (which is coplanar with the circle). R is the "major radius" of T, and r is the "minor radius." Intersecting the torus T with a plane parallel to its axis gives a plane curve, called a "spiric section of Perseus." In the special case where this intersecting plane is at distance |R - r| from the axis, so it is also a tangent plane, the curve is called a "hippopede of Proclus."

These curves are a topic of my joint paper with Marc Frantz:

doughnuts --- is there anything they can't do? When r < R, the hippopede has a double point.

It is also called a "hyperbolic lemniscate of Booth," and it is the image of a hyperbola under inversion with respect to its center.

A spiric section where the plane is at distance r from the axis is called an "oval of Cassini." The only oval of Cassini which is also a hippopede of Proclus is at r = |R - r|, so r = R/2. This curve is the "lemniscate of Bernoulli."

When r = R, the hippopede is a pair of externally tangent circles.
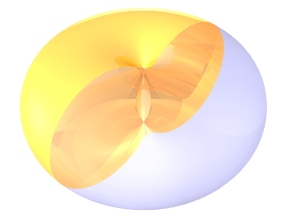
When r > R, the torus intersects itself. The hippopede becomes the union of a smooth curve and an isolated point (an "acnode" of the curve, where the plane is tangent).

This curve is also called an "elliptic lemniscate of Booth," and it is the image of an ellipse under inversion with respect to its center.

When r is large compared to R, the smooth curve's interior becomes convex, but a hippopede is never equal to an ellipse (nor does it have any ellipse as a subset, except the circles in the r = R case). As r/R tends to infinity, the curve approaches a circular shape.
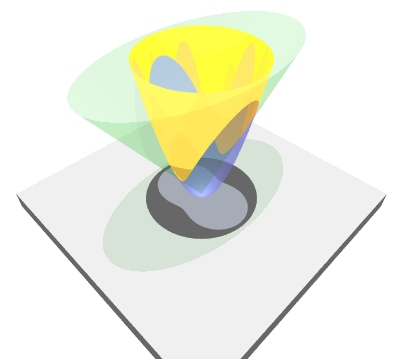
The elliptic lemniscate can also be described as a projection of the space curve formed by the intersection of a circular paraboloid and an elliptic cone, with the same vertex and axis.
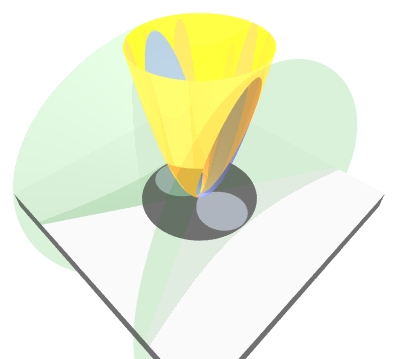
The hyperbolic lemniscate is equal to a projection of the space curve formed by the intersection of a circular paraboloid and an elliptic cone, with the same vertex and perpendicular axes.
Here's a link to an animation: 1,145KB gif

Links

Back to the graphics gallery.