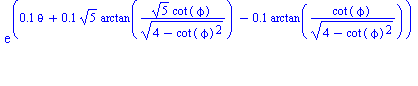An "equiangular surface"
as defined by K. Boyadzhiev
Reference: K. Boyadzhiev, Equiangular surfaces, self-similar surfaces, and the geometry of seashells, College Math. Journal (4) 38 (2007), 265 - 271.
Maple code:
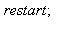

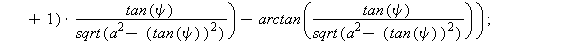
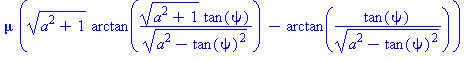
| > |
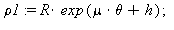 |
![(Typesetting:-mprintslash)([rho1 := R*exp(mu*theta+mu*((a^2+1)^(1/2)*arctan((a^2+1)^(1/2)*tan(psi)/(a^2-tan(psi)^2)^(1/2))-arctan(tan(psi)/(a^2-tan(psi)^2)^(1/2))))], [R*exp(mu*theta+mu*((a^2+1)^(1/2)...](images/equiang_6.gif)
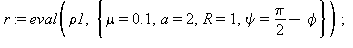
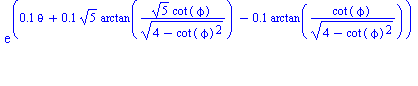

POV-Ray picture:
(exported from Maple)

![]()
![]()
![]()
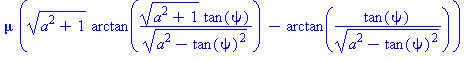
![(Typesetting:-mprintslash)([rho1 := R*exp(mu*theta+mu*((a^2+1)^(1/2)*arctan((a^2+1)^(1/2)*tan(psi)/(a^2-tan(psi)^2)^(1/2))-arctan(tan(psi)/(a^2-tan(psi)^2)^(1/2))))], [R*exp(mu*theta+mu*((a^2+1)^(1/2)...](images/equiang_6.gif)
![]()